Производная и первообразная функции
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
1. Вычисление производной функции
Правила дифференцирования

Дифференцирование сложной функции

Таблица производных

Первообрáзной или примити́вной функцией данной функции  называют такую
называют такую  , производная которой (на всей области определения) равна
, производная которой (на всей области определения) равна  , то есть
, то есть 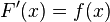 . Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
 называют такую
называют такую  , производная которой (на всей области определения) равна
, производная которой (на всей области определения) равна  , то есть
, то есть 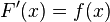 . Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
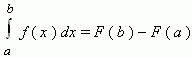
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).
Комментариев нет:
Отправить комментарий